WordWalk Puzzles

 This puzzle is for the rootword 'artistic' and the subwords: ' rat','tars','trait','tiaras'. The stages of solving are presented in vertical image frames, thanks to ImageMagick's convert -append utility:  

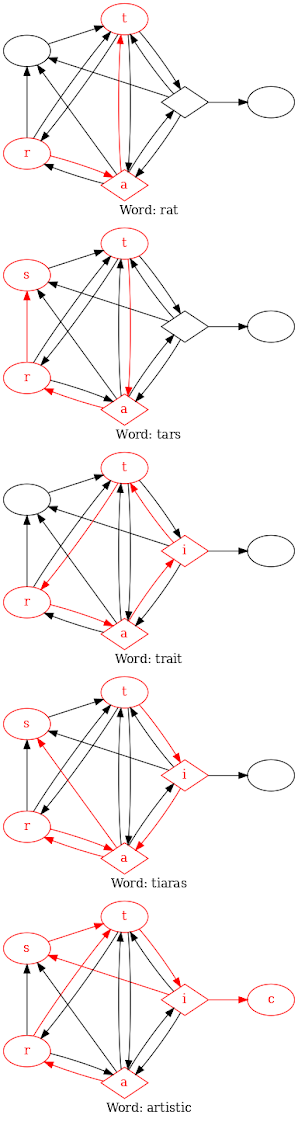
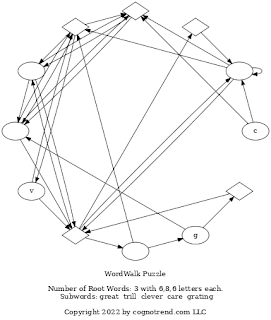
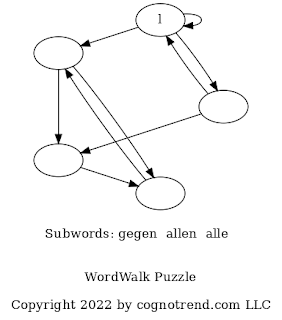
 It turns out that some WordWalk puzzles have different solutions.  That's because many different can have the same set of unique letters.  E.g., the words 'earth', 'heart', 'rather', 'theater', 'threat' all use the same unique set of letters {e,a,r,t,h}, although some words use multiple instances of the same letter.  'theater', for instance, use e and t twice each. I call such words equivalent to each other.  Here's another set of equivalent words:{'pressure', 'purse', 'pursue', 'super'} And yet another: {'concentration', 'container', 'creation', 'interaction', 'reaction'} If a WordWalk puzzle is built from any one of a set of equivalent words, it may have the same structure (i.e., be isomorphic) as one built from another from the same set of equivalent words -- but not necessarily!  The nodes will certainly be the same, but the arrows may be different.   Con...

 Although I haven't verified this empirically yet, it seems that many German words are capable of generating a great number of subwords, perhaps more so than English. For instance, the from the German word 'abend' (evening) the following subwords can be generated: "ab ade an bad bade band bann beben benennen da dann dannen den denen denn eben ebene ebne ebnen end ende enden na neben nenn nenne nennen" For a total of 27 subwords.   One must keep in mind, however, that German is an inflected language with multiple word forms for each noun, verb, adjective and adverb.  This can be seen from the list above. German is also notorious for having many very long words, like 'allerliebstgeselliger'.  Naturally, this puppy has a humongous number of subwords -- 597 in the word list I compiled from three fairly archaic sources.  Nonetheless, the list is amazing: "aar aas ab aber abgelegt aglaia all allalle allbereits alle allee aller allerbeste allerlei allerliebs...

 Most of the WordWalk puzzles published on the WordWalk website are generated from a single root word.  However, it is possible to generate them from a list of root words. Doing so generally adds more nodes and arrows. Consider the example below formed from the root words 'violin', 'clarinet', and 'guitar' and also the subwords 'great', 'trilling', 'clever', 'care': The first letters of each of these root words is indicated.  (Notice also that I'm indicating vowel locations by diamond node shapes.) Here's the location of the subword 'great': You'll notice that 'great' is not subword of any one of the three root words, but its set of letters is a subset of the union of the set of letters taken from the root words. Thus finding a subword like this will only yield partial information about each root word. Here's the location of 'trilling': Likewise for 'care' and 'clever': And ...

If you are interesting in testing your knowledge of German words and solving some WordWalk puzzles, please see the  website . This is a collection of 25 puzzles of intermediate difficulty.

WordWalk puzzles can be generated in any language that has an alphabet. Consider the German word 'lange'  (= 'long' in  English) as the root word.  Given the subwords 'gegen', 'allen', and 'alle', we can generate the puzzle: (Note, however, that we have not used diamond shapes for vowel nodes.)  The solution to this  

WordWalk puzzles are word games based on the directed graphs inherent in the spelling of words (in any language that supports alphabetical spelling).  The idea is that the sequence of letters in each word implies a unique directed graph that is unique for the given word.  Letters are assigned unique vertices in the graph and the relation 'is-followed-by' between letters is reflected in a directed graph edge. For example, the word 'jump' would be represented as the graph <V,E> where V={j,u,m,p} and E={(j,u),(u,m),(m,p)}. Pictorially, we might have: (The special diamond shape for the letter 'u' is used in official WordWalk puzzles to indicate that this letter is a vowel.) This directed graph contains only a single path and is perhaps not very interesting because each letter occurs exactly once.  But if a letter occurs more than once, an arrow is drawn from the letter just before the repeat back to the original node for that latter.  E.g.,in the word 'el...