Optimal Parameters

The parameters I use in generating the WordWalk puzzles are the following:

1)  The length of the rootword (i.e., the number of letters in the rootword)

2)  The number of subwords to use

3)  The minimum length of each   

The goal for setting these parameters is to ensure that the resulting puzzle is not too hard and not too easy.

If there are too many subwords, the chances are good that all the letters and all the arrows will already be present in the subwords, thus making the puzzle too hard, because there will be no unused arrows to hint at those used in the rootword.  

If the number of subwords is too low, most of the arrows will be used up only by the rootword, making it almost a pure guessing game;  then the game is too hard and not too interesting.  

The game is most interesting, I think, when you have to do some logical reasoning by looking at the unused arrows and eliminating some of the possibilities.  The unused arrows provide hints as to digramms and trigramms used in the root word.

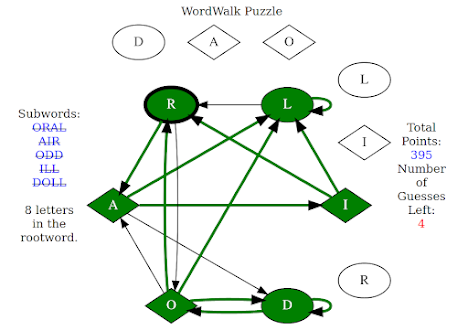
Here's an example:

All the subwords have been traced out; only the rootword remains to be found.  It has 8 letters, but only six distinct letters are used;  so two letters are reused, perhaps consecutively, perhaps not.

If you examine the used arrows starting with R, you'll that O-A-D follow immediately, leading you to believe that the rootword begins with the subword "ROAD".  But this turns out to be misleading, for R may -- and indeed does -- occur twice in the rootword.  

Another hint is that the digramm L-R must be in the rootword.  Thus, possibly, the sequence L-R-O-A-D is in the root word. 

So what word begins with R and possibly ends with L-R-O-A-D?  

I'm sure you've guessed it by now:  It's RAILROAD!

Comments

Post a Comment

Popular posts from this blog

New WordWalk Format

Image
 Yesterday we implemented a new version of WordWalk , eliminating the drag-and-drop approach in favor of point-and-click.   We have also placed all the candidate letters in a table row above the graph, so now there are no longer any floating letters that have to be dragged and dropped. We have also included the maximum possible score (which varies with each puzzle) so that you can compare your score against the best possible. To help understand how this works, let take a look at the kid's puzzle step by step. Here's the initial set up. Note that there 395 points possible. First we try to spell out "BEER" by selecting the B in the table: Then we select the B in the graph, which gets highlighted in yellow, and the yellow/red coloring for the B in the table reverts to white/black: Since the B is a correct first letter for either of the subwords, it remains yellow/black until the subword is completed.  Since we are trying for "BEER", the next letter is E: Placin...
Read more

A New Feature

Image
WordWalk puzzles now highlight the letter that starts the hidden rootword by thickening the border of the shape that depicts it. This was due to discovering that it is easy to forget which letter was first after correctly placing the subwords in the graph. E.g.,in today's English puzzle, we have: The first letter of the rootword is H, as indicated by the ovals with the thick borders.  Then, after embedding, e.g., the subword "HALL" into the puzzle, we can still tell which letter is the first letter of the rootword:
Read more

WordWalk Puzzles and Graph Theory

Image
WordWalk puzzles are word games based on the directed graphs inherent in the spelling of words (in any language that supports alphabetical spelling).  The idea is that the sequence of letters in each word implies a unique directed graph that is unique for the given word.  Letters are assigned unique vertices in the graph and the relation 'is-followed-by' between letters is reflected in a directed graph edge. For example, the word 'jump' would be represented as the graph <V,E> where V={j,u,m,p} and E={(j,u),(u,m),(m,p)}. Pictorially, we might have: (The special diamond shape for the letter 'u' is used in official WordWalk puzzles to indicate that this letter is a vowel.) This directed graph contains only a single path and is perhaps not very interesting because each letter occurs exactly once.  But if a letter occurs more than once, an arrow is drawn from the letter just before the repeat back to the original node for that latter.  E.g.,in the word 'el...
Read more